А что если автор "Алисы в Стране чудес" вовсе и не заступал в долины подсознательного в своем произведении, а просто выразил свое отношение к современным ему процессами в математической науке таким вот необычным и замысловатым образом? Все-таки он был преподователям Царицы наук, а не психиатором. Читаем и решаем сами, согласиться ли с автором поста или все-таки, по старинке, с группой Jefferson Airplane.
Знаменитая «Алиса в стране чудес» Льюиса Кэрролла была бы совсем другой книгой без Чеширского Кота, описания суда, «ребёнка» Герцогини и без Безумного Чаепития в компании Болванщика. Однако, если познакомиться с оригиналом той сказки, которую автор рассказал Алисе Лиддел и двум ее сестрам однажды на лодочной прогулке близ Оксфорда, то вы не найдете в тексте всех этих знаменитых персонажей и символов.
Когда я взялась за написание диссертации, посвящённой английской литературе викторианской эпохи, я хотела выяснить, что вдохновило автора на все эти более поздние дополнения. В критической литературе книга, как правило, интерпретируется во фрейдистском ключе как стремительный спуск в темные глубины подсознания. Подробный анализ добавленных сцен мне не попадался, но одна работа сильно выделялась на фоне остальных. В 1984 году Хелена Пайсиор из университета Висконсин-Милуоки написала статью, в которой проследила связи между судом над Червонным Валетом с викторианским учебником алгебры. Учитывая основную специальность автора «Алисы», было довольно удивительно обнаружить, что почти не существует исследований его книги с математической точки зрения. Как известно, «Кэрролл» – это псевдоним. Настоящее имя автора – Чарльз Доджсон, он работал преподавателем математики в оксфордском колледже Крайст-Чёрч.
Для математики XIX век выдался очень бурным, породил множество новых и неоднозначных концепций, которые, однако, были широко восприняты в научном сообществе. Если рассмотреть «Алису в стране чудес» именно в таком контексте, становится понятно, что математик Доджсон, отличавшийся редкостным консерватизмом, придумал некоторые сцены, отсутствующие в первой редакции сказки, чтобы высмеять эти радикально новые идеи.
Даже самые восторженные поклонники Доджсона вынуждены признать, что тот был очень осторожным математиком и оставил совсем мало оригинальных работ. Однако он был добросовестным педагогом и из всех математических работ превыше всего ценил древнегреческий евклидовский трактат «Начала», который считал образчиком математического мышления. В целом этот труд Евклида посвящён геометрии окружностей, четырёхугольников, параллельных прямых, а также затрагивает простейшие тригонометрические функции. Но самая поразительная черта «Начал» заключается в исключительной строгости рассуждений. Евклид начинает книгу с изложения нескольких неопровержимых истин (аксиом), а затем выстраивает на их основе сложные доказательства. При этом каждый шаг доказательства остается простым и логичным. Каждая посылка постулируется, доказывается, а каждая такая теорема резюмируется «Что и требовалось доказать».
Веками такой подход считался вершиной математического и логического мышления. Однако, к разочарованию Доджсона, не все математики его века отличались евклидовской скрупулёзностью. Доджсон отвергал их работы как «полудилетантские» и даже считал не вполне логичными. Тем не менее, к разочарованию Доджсона, эта новая математика все сильнее отдалялась от физической реальности, на основе которой были построены труды Евклида.
В настоящее время ученые широко используют математические концепции, которые на первый взгляд кажутся нелогичными, например, мнимые числа. Мнимое число представляет собой квадратный корень из отрицательного числа и описывает физические величины совсем не так, как целые числа или дроби. В викторианскую эпоху еще никто не воспринимал эти новые концепции безоговорочно, шли отчаянные поиски философской базы, которую можно было бы подвести под эти феномены. Однако такие разработки открывали перед математиками удивительные возможности для исследования новых идей. Многие были готовы вооружиться этой странной логикой, поскольку существовал вполне непротиворечивый научный аппарат для операций над такими концепциями. Тем не менее, с точки зрения Доджсона, новая математика была абсурдна. Он признавал, что все эти наработки могут быть интересны маститому ученому, но был уверен, что все это невозможно объяснить обычному студенту.
В научной периодике Доджсона просто разгромили, и он решил подойти к математике через художественную литературу. Вооружившись методом, знакомым из доказательств Евклида – доведением до абсурда, – он раскритиковал «полулогичность» новой математики. Доджсон высмеял ее слабые стороны, доведя заложенные в ней посылки до логического завершения и ожидаемо получив абсурдные результаты. Так появилась книга «Алиса в стране чудес».
Алгебра и кальян
Обратимся, например, к главе «Синяя гусеница даёт совет». Алиса уже успела упасть в кроличью нору и съесть пирожок – в том эпизоде девочка уменьшилась до трёх дюймов. А в пятой главе, которую мы решили перечитать, автор знакомит нас с Гусеницей, которая курит кальян. Гусеница показывает Алисе гриб: чтобы вернуть нормальные размеры, девочке нужно им полакомиться. Но вся загвоздка в том, что мякоть с одной стороны гриба вытягивает Алисину шею, а с другой стороны – укорачивает туловище. Чтобы вернуть себе нормальные размеры и пропорции, Алиса должна откушать строго определенное количество мякоти с каждой стороны гриба.
Некоторые исследователи считают, что эта сцена с кальяном и «волшебным грибом» намекает на наркотики. Однако, я полагаю, здесь Доджсон излагает свои представления об абсурдности символической алгебры, которая разрывала связи между алгеброй, арифметикой и излюбленной геометрией Доджсона. В следующих главах книги содержатся более специфические математические аналогии, но эта сцена легкая и игривая. Она задает тон для того сюра, который ждет читателя впереди.
Первый намёк может быть связан с самим кальяном: начнем с того, что в английском языке кальян называется словом «hookah», которое имеет арабское происхождение, как и слово «алгебра». Тем более интересно отметить, что Огастес де Морган, первый британский математик, сформулировавший непротиворечивый аппарат правил символической алгебры, использует в своей книге «Тригонометрия и дважды алгебра» (1849) оригинальное арабское название алгебры. Морган употребляет формулировку «al jebr e al mokabala» [аль джебр э аль мокабала], что означает «сокращение и восстановление» – фактически, именно это и претерпевает Алиса. Именно стремление к «восстановлению» привело Алису к грибу: она искала, чего бы такого съесть или выпить, чтобы приобрести нормальный размер. Когда она съела кусочек гриба, с ней произошло как раз «сокращение» – подбородок стукнулся о ноги.
В своей работе де Морган описывает, почему хочет отойти от универсальной арифметики, где алгебраические символы означают конкретные числа, соответствующие физическим величинам. Он предпочитает такой системе символическую алгебру, где допускаются любые «абсурдные» операции, в том числе, приводящие к отрицательным или невозможным решениям. Главное, чтобы эти операции следовали четкой внутренней логике. Именно символическая алгебра сегодня стала отточенным языком для описания отношений между математическими объектами, но в викторианскую эпоху алгебра воспринималась совершенно иначе. В первых работах по символической алгебре также сохранялась косвенная связь с физическими величинами.
Де Морган желал устранить даже эту зыбкую связь с измерениями и предлагал трактовать символическую алгебру как грамматическую систему. Достаточно «сократить» алгебру от универсальной арифметики до набора логических, но при этом совершенно символических операций, считал он, и мы сможем «восстановить» более глубокий смысл всей системы. Правда, на тот момент он ещё не мог сказать как.
Алиса, держи себя в руках
Я полагаю, что абсурдность Страны Чудес отражает представления Доджсона об опасностях новой символической алгебры. Алиса попадает из рациональной реальности в мир, где даже числа действуют беспорядочно. В зале, куда ее привела кроличья нора, Алиса пытается припомнить таблицу умножения, но оказывается, что ее расчёты не вписываются в привычную систему с основанием 10. В сцене с гусеницей Доджсон выражает свои опасения, рассказывая, что Алисин рост колеблется между 9 футами и 3 дюймами. Алиса скована рамками традиционной арифметики, где физическая величина (например, размер) должна быть определенной. Алису это сильно беспокоит. «Столько превращений в один день хоть кого собьет с толку», – жалуется она. «Не собьет», – возражает Гусеница. Действительно, она же привыкла жить в абсурдном мире.
Предостережение, которое Гусеница изрекает в конце этой сцены, вероятно, один из самых красноречивых намеков на доджсоновкую консервативную математику. «Держи себя в руках!» – заявляет Гусеница. Алиса предполагает, что Гусеница рекомендует ей не злиться. Однако, хотя девочка действительно выражается достаточно резко, к этому моменту она не успела сказать ничего обидного, поэтому достаточно странно, что совет Гусеницы звучит именно так. В оригинале же гусеница говорит: «Keep your temper». Интеллектуалы времен Доджсона, вероятно, должны были понять слово «temper» (умеренность) в буквальном смысле: «пропорция, где все свойства находятся в правильном соотношении». Таким образом, Гусеница подсказывает Алисе, что сохранять умеренность – это придерживаться правильных пропорций, независимо от того, каков твой размер.
Здесь, опять же, прослеживается любовь Доджсона к евклидовой геометрии, где абсолютная величина не имеет значения. По-настоящему важны лишь соотношения длин отрезков, например, при определении свойств треугольника. Чтобы уцелеть в Стране Чудес, Алиса должна действовать, как геометр-евклидианец, – сохранять пропорции, даже если её размеры меняются.
Разумеется, она этого не делает. Алиса съедает кусочек гриба, и её шея вырастает, как у змеи, что приводит к новому витку абсурда, пока Алиса не исправляет свой рост, откусив от гриба с другой стороны. Это важная присказка для следующей главы «Поросёнок и перец», где Доджсон пародирует еще один тип геометрии.
К этому моменту Алиса уже вернулась к своим нормальным размерам, но затем девочка снова уменьшается, чтобы попасть в маленький домик. Там на кухне она встречает Герцогиню, баюкающую ребёнка. Кухарка сыплет в суп слишком много перца, и от запаха супа чихают все, кроме Чеширского Кота. Но когда Герцогиня даёт Алисе подержать ребенка, тот почему-то превращается в поросенка.
Весь этот эпизод посвящён проективной геометрии, которая исследует свойства фигур. Эти свойства не изменяются, даже если фигура проецируется на другую плоскость. Допустим, изображение выводится на подвижный экран, а затем мы наклоняем этот экран под разными углами, получая семейство фигур. В этой дисциплине присутствуют различные феномены, многие из которых Доджсон, вероятно, считал нелепыми. Типичным примером такого феномена является «принцип непрерывности».
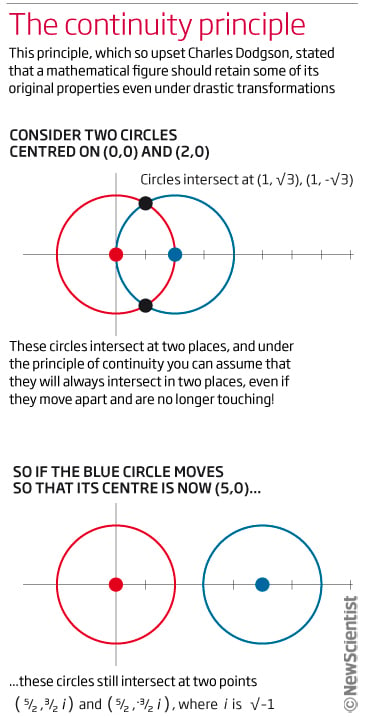
Жан-Виктор Понселе, математик, предложивший этот принцип, формулирует его следующим образом: «Если одна фигура получается из другой непрерывным преобразованием и полученная фигура не уступает по общности исходной, то можно сразу же утверждать, что любое свойство первой фигуры будет справедливо и для второй фигуры».
Пожалуй, простейшим примером этого принципа является соотношение двух пересекающихся окружностей. Решив их уравнения, мы найдем, что они пересекаются в двух разных точках. Согласно принципу непрерывности, любое непрерывное преобразование этих окружностей, например, удаление их центров друг от друга, не нарушает вышеуказанного базового свойства, а именно: окружности так и будут пересекаться ровно в двух точках. Лишь если центры окружностей будут удалены друг от друга достаточно сильно, решение задачи будет включать мнимое число, которое нельзя выразить в «физическом» смысле.
Разумеется, когда Понселе говорит о «фигурах», он имеет в виду геометрические фигуры. Но в английском языке слово «figure» также означает «персонаж», и Доджсон шутливо подвергает «полудилетантский» аргумент Понселе строгому логическому анализу, доводя его до самого абсурдного вывода. Если принцип действует на треугольники, значит, он должен действовать и на младенцев. Если нет – сам принцип является ошибочным. Что и требовалось доказать. Итак, Доджсон превращает младенца в поросенка в соответствии с принципом непрерывности. Примечательно, что это существо сохраняет большую часть своих основных черт, что полностью согласуется с принципом непрерывности. Например, его ручки и ножки по-прежнему торчат в разные стороны, как лучи морской звезды, малыш все изгибается, нос у него слишком вздернутый для младенца, а глазки – слишком маленькие. Алиса осознает, что произошло, только когда плач младенца сменяется хрюканьем. Все происходящее доставляет малышу огромное неудобство, а несдержанная жестокость Герцогини ярко демонстрирует ядовитый скепсис Доджсона относительно «современной» проективной геометрии. В главе о поросёнке и перце абсолютно всё идет наперекосяк. Герцогиня – плохая аристократка и никуда не годная мать, Кухарка – плохая повариха, которая задымляет всю кухню, переперчивает суп и, в конце концов, начинает бросаться кочергой, горшками и тарелками.
Алису злит вся эта кутерьма, она покидает дом Герцогини и отправляется на чаепитие к Болванщику. Здесь автор препарирует работы ирландского математика Уильяма Роуэна Гамильтона. Гамильтон умер в 1865 году вскоре после публикации «Алисы в стране чудес». Но в тот период всё ещё широко обсуждалось открытие кватернионов, сделанное Гамильтоном в 1843 году. Это открытие считалось важнейшей вехой в истории абстрактной алгебры, поскольку кватернионы обеспечивали алгебраическое вычисление вращений.
Как известно, комплексное число состоит из двух частей. Кватернионы существуют в такой математической системе, которая основана на использовании четырех частей (см. «Мнимая математика»). Гамильтон долгие годы разрабатывал трехчастную систему – по одной части на каждое пространственное измерение, – но ему удавалась лишь модель вращения на плоскости. Но, когда он добавил четвертую часть, удалось, наконец, представить трехмерное вращение. Правда, Гамильтон затруднялся описать, чему же соответствует дополнительная четвертая часть. Как и большинство викторианцев, он был уверен, что эта часть должна что-то означать. Поэтому в предисловии к своим «Лекциям о кватернионах» (1853) он сделал примечание: «Мне казалось (и по-прежнему кажется) естественным соотнести эту внепространственную часть с феноменом времени».
Гамильтон полагал, что если геометрия обеспечивает исследование пространства, то алгебра, в свою очередь, позволяет изучать «чистое время». Это довольно запутанная концепция, которую Гамильтон сформулировал на основе идей Канта. Предполагалось, что «чистое время» представляет собой идеал времени в платоновском смысле и отличается от реального времени, воспринимаемого людьми. Другие математики вежливо, но осторожно относились к этой гипотезе, считая, что «идеальное время» – это уже слишком. Между математикой Гамильтона и чаепитием у Башмачника прослеживаются поразительные параллели. Алиса сидит за столом с странными персонажами: Болванщиком, Мартовским Зайцем и Мышью-соней. Персонаж Время, который поссорился с Болванщиком, отсутствует. Но из вредности Время не позволяет стрелкам часов Болванщика дойти до шести вечера и продвинуться дальше.
Если интерпретировать эту сцену в контексте математики Гамильтона, можно сделать вывод, что трое персонажей соответствуют трем частям кватерниона, а важнейшая четвертая часть – Время – отсутствует. Автор объясняет нам, что без Времени вся троица навечно застряла за чаепитием, и они «даже посуду мыть не успевают».
Их суета вокруг стола напоминает о первых попытках Гамильтона вычислить движение, которое сначала (до добавления в систему четвертой части – Времени) удавалось смоделировать лишь на плоскости. Даже когда Алиса присоединяется к чаепитию, она не может остановить возню Болванщика, Зайца и Сони, так как девочка не является внепространственной единицей, подобной Времени.
В этой сцене Болванщик загадывает абсурдную загадку: «Чем ворон похож на конторку?» Этот эпизод более чётко указывает на теорию «чистого времени». Гамильтон утверждал, что на уровне чистого времени исчезает связь между причиной и следствием, и, возможно, именно на это указывает безумность загадки Болванщика, на которую не может быть ответа. Алиса смело пытается отгадать загадку, и здесь автор высмеивает еще одно свойство кватернионов. Дело в том, что умножение кватернионов некоммутативно, то есть, x × y не равно y × x. Ответы Алисы также некоммутативны. Когда Заяц заявляет, что «нужно всегда говорить то, что думаешь», Алиса отвечает: «Я так и делаю… По крайней мере, я всегда думаю, что говорю… а это одно и то же». «Совсем не одно и то же!, – возражает Болванщик. – Так ты еще, чего доброго, скажешь, будто «Я вижу то, что ем» и «Я ем то, что вижу» – одно и то же». Вероятно, подобные идеи должны были раздражать математика-консерватора наподобие Доджсона, поскольку некоммутативная алгебра противоречит основополагающим законам арифметики и открывает удивительный мир новой математики – даже еще более абстрактный, чем тот, который описали сторонники символической алгебры.
В финале этой сцены Болванщик и Заяц засовывают Соню в чайник. Возможно, это путь к свободе. Если бы парочка смогла избавиться от Сони, то могла бы существовать независимо – как двухчастное комплексное число. Это тоже безумие, считает Доджсон, но тогда, по крайней мере, можно будет не двигаться кругами вокруг стола (то есть, не вращаться).
Здесь, вероятно, сатирические выпады Доджсона против современников-математиков заканчиваются. Что же остается в сказке «Алиса в стране чудес» без этих аналогий? Ничего кроме исходной доджсоновской сказки на ночь «Приключения Алисы под землей». Эта сказка очаровательна, но совершенно лишена всякого характерного нонсенса. Доджсон демонстрирует верх остроумия именно когда высмеивает что-либо, но он пускается в сатиру, лишь если тема донельзя его задевает. Он написал два уморительно смешных памфлета, в которых ерничал над новыми порядками в Оксфордском университете. Напротив, все его истории, кроме «Алисы», были скучны и нравоучительны.
Готова поспорить, что не будь в «Алисе» яростной сатиры, с которой Доджсон обрушился на своих коллег-математиков, эта книга никогда не стала бы такой знаменитой, а Льюиса Кэрролла никто бы не помнил как непревзойденного мастера сюрреалистической сказки.
Перевод статьи Мелани Бейли
Иллюстрация: wikipedia.org
Релоцировались? Теперь вы можете комментировать без верификации аккаунта.