

Как фракталы и кривая Серпинского в частности могут помочь в обработке сейсмологических данных? А очень просто, считает автор этого поста.
В отличие от меня, моя жена занимается на компьютере важной работой – выполняет серьезные вычисления для ответа на важные вопросы. Одна из таких проблем – получение перекрестных корреляций многочисленных сейсмологических данных, собираемых на сотнях измерительных станций. Вычисления могут занимать целые дни и даже недели. Интересно отметить, что значительная часть этого времени уходит на загрузку данных с дисков в память. Чтобы лучше понять данную проблему, давайте в общей перспективе рассмотрим, как такие перекрестные корреляции реализуются в псевдокоде, напоминающем Python:
# имеем некоторый список станций, допустим, список имен с файлами данных stations = [..] # поочередно определяем корреляцию каждой уникальной пары станций for i in range(len(stations)) : for j in range(i+1, range(len(stations))) : # ниже коррелируются одновременно две пары: (i,j) и (j,i) computation(stations[i], stations[j])
Данный псевдокод обходит все возможные комбинации двух станций и вычисляет так называемую «перекрестную корреляцию». Сигнал каждой станции представлен в виде большого файла данных, который сохраняется на диске. Этот файл требуется загрузить на диск для вычисления корреляции. Загрузка в память с диска – затратная операция, поскольку даже самые современные диски работают медленно по сравнению с современными процессорами и оперативной памятью. К счастью, система кэширует данные – то есть, переиспользует информацию, уже имеющуюся в системе, а не загружает ее заново снова и снова. Но мощность памяти в системе ограничена, а в разделяемой системе, к тому же, является переменной. Если память заполнится до отказа, а в нее потребуется записать новые данные, то такая актуальная информация заменит собой часть данных, уже имеющихся на диске – тех, которые уже давно не используются.
Соответственно, порядок, в котором мы обращаемся к информации отдельных станций – так называемое «расписание» – определяет количество обращений к диску. Требуется подобрать такое расписание, которое минимизирует число таких операций считывания и позволяет максимально активно использовать кэш. Более того – что делать, если точный размер памяти неизвестен?
Два года назад я обнаружил, что фрактальная кривая Серпинского дает хорошее и, пожалуй, асимптотически оптимальное расписание. Я переписал некоторые эксперименты с корреляцией на языке программирования Elm (чисто для интереса, но, надеюсь, и вам понравится), поставив перед собой задачу представить красивую кривую Серпинского и ее дискретизированный аналог – H-индекс.
Вычисление затратности расписания
Расписание можно визуализировать как путь, проложенный через квадратную матрицу, где каждая ячейка состоит из комбинации двух станций. Такая комбинация называется «задачей». При обходе нужно пройти лишь через верхний (или нижний) треугольник в матрице, так как (3,4) равноценно (4,3). Вышеприведенный псевдокод определяет следующее расписание, которое называется «построчным» (scanline).
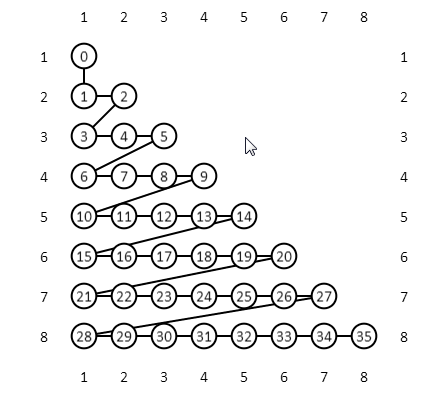
Соответственно, показанное здесь расписание первым делом соотносит станцию 1 с ней же, затем 1 с 2, далее 2 с 2 и т.д. Затратность этого расписания – то есть, количество обращений к диску или кэш-промахов – можно рассчитать, симулировав выполнение, отслеживая, в то же время, содержимое кэша и подсчитывая, сколько раз приходится загружать данные со станции, пока еще отсутствующие в памяти. При запуске такой симуляции (где память способна вместить пять элементов) получается следующая совокупная затратность для всех последовательных выполнений.
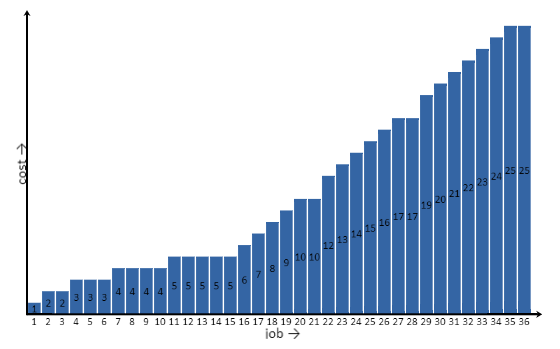
Совокупная затратность демонстрирует, что вначале (до 15 элементов) построчное расписание работает хорошо. Но как только протяженность расписания по горизонтали превышает 5 единиц, каждая новая задача дает кэш-промах. На самом деле, можно решить задачу гораздо эффективнее, не допуская горизонтальных «пролетов» шире 5 единиц.
Попробуйте с нижеприведенным планировщиком! Щелкайте по кружочкам в матрице для назначения задач. В правом верхнем углу находятся символы «+» и «-», с их помощью можно повышать и понижать объем памяти. Наша цель – уменьшить суммарную затратность всего расписания.
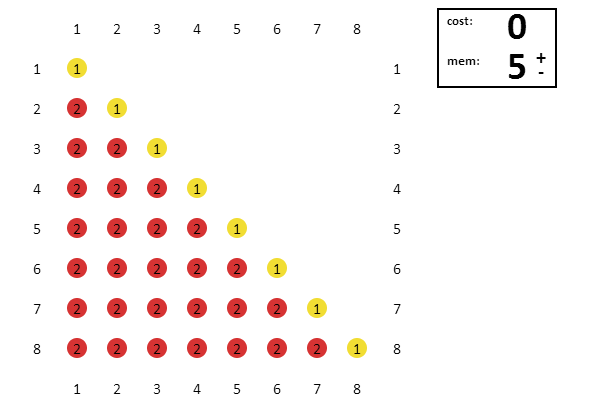
Чтобы вам было легче построить путь, неназначенные элементы в пути отмечены и обозначены цветами в зависимости от их стоимости.
Кривая Серпинского или H-индекс
Оказывается, совсем не просто найти оптимальное расписание, требующее минимального количества обращений к диску. Немного поэкспериментировав, мы также обнаруживаем, что производительность расписания значительно изменяется в зависимости от объема памяти. Это усложняет нашу задачу, в особенности с учетом того, что в процессе выполнения объем памяти может меняться. Например, такие изменения будут происходить, если корреляции подсчитываются на суперкомпьютере, который вы используете совместно с другими учеными, выполняющими схожие эксперименты.
Однако, быстро выясняется, что, как правило, не следует делать больших скачков. Соответственно, требуется составить такое расписание, в котором наиболее свежие задачи расположены в матрице поблизости друг от друга. Данное наблюдение наталкивает нас на использование стратегии «разделяй и властвуй». Это означает, что мы разбиваем большой треугольник на более мелкие и сначала выполняем задачи из первого треугольника, потом – из второго и так далее. Рекурсивно применяя этот шаблон, получаем такую последовательность:
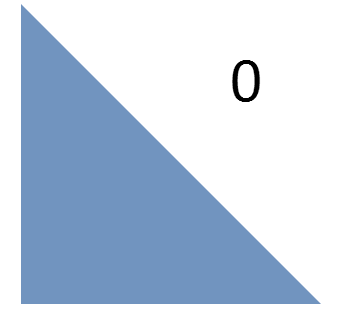
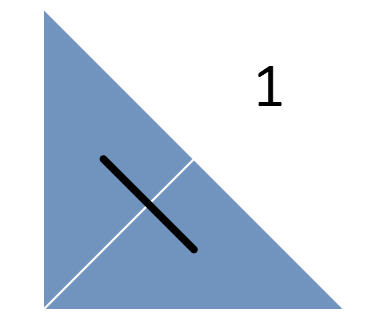
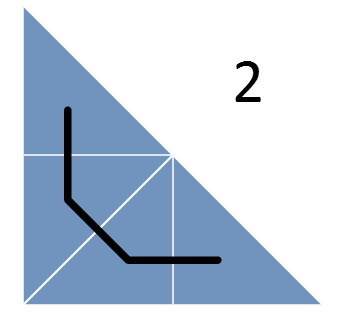
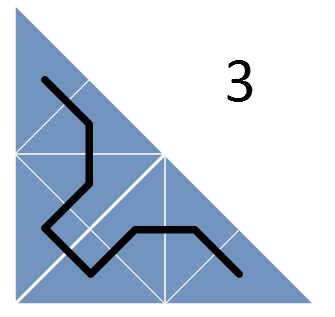
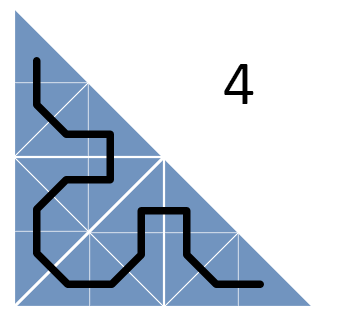
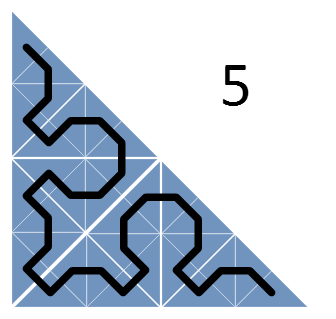
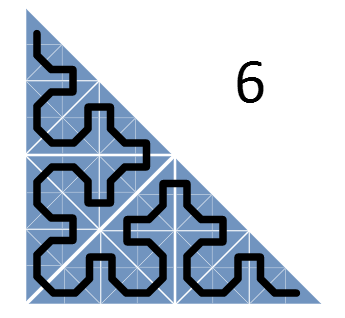
Кроме разбиения треугольников проводится линия, попадающая в каждый из треугольников всего по разу. Эта линия представляет собой кривую Серпинского (вернее, ее нижний треугольник) – фрактальную кривую, в которой непрерывно происходит разбиение на все более мелкие треугольники, причем эта кривая ни разу не пересекает сама себя.
Теперь рассмотрим треугольник задач, которые требуется назначить, и рекурсивно будем разбивать его на более мелкие, пока одному треугольнику не будет соответствовать ровно одна задача. Кривая Серпинского, проходящая через треугольники, описывает наше расписание!
Однако, решение неполное: ведь разбивать задачу нельзя, поэтому наша модель не позволяет ровно распределить задачи по треугольникам. Нам потребуется дискретная разновидность кривой Серпинского, которая именуется «H-индекс». В данном контексте «индекс» - синоним «расписания», а буква «H» напоминает контур, вырисовывающийся при применении данного шаблона: в нижнем правом углу сбоку от контура заметна именно такая фигура. H-индекс определяет следующее расписание:
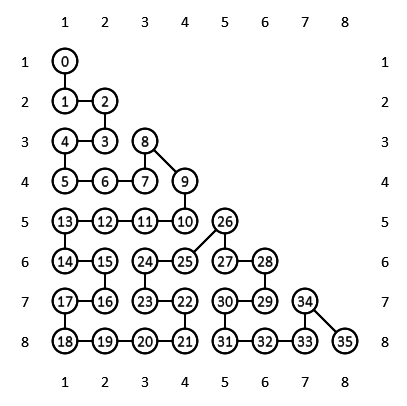
Важное достоинство H-индекса заключается в его замечательной локальности. Любые две задачи, назначенные плотно друг к другу (с небольшим временным интервалом) также будут находиться поблизости и в матрице задач. Локальность важна потому, что те задачи, которые соседствуют друг с другом в таком расписании, с высокой вероятностью окажутся в кэше.
Насколько выгоднее работать с H-индексом? На следующем графике затратность показана в зависимости от кэш-промахов в каждом варианте расписания. Рассмотрен случай с 64 станциями и, соответственно, 576 задачами при увеличении объема памяти.
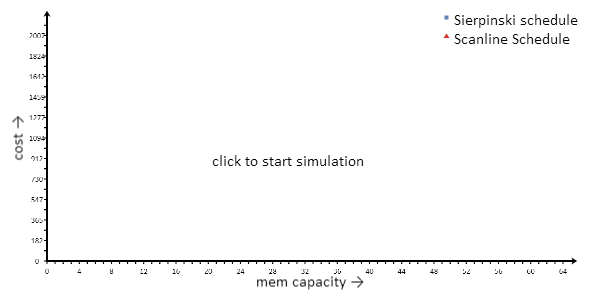
Рассмотрен диапазон, ограниченный значениями 2 и 64: в памяти необходимо сохранить как минимум две станции. Если мощность памяти допускает размещение информации о 64 станциях, то затратность всех расписаний будет равна 64, поскольку каждую задачу потребуется загрузить ровно один раз. Стоимость такого построчного алгоритма определяется линейным отношением, которое также наблюдается в последней части (после задачи 16) предыдущего графика. Также можно отметить, что H-индекс работает лучше, если объем памяти равен степени 2. Особенно следует отметить низкие значения: 4, 8 и 16. Между этими точками H-индекс становится немного нерегулярным, но в целом кривая графика быстро приближается к минимальному количеству загрузок.
Заключение
Надеюсь, конечный вариант графика убедительно показывает, что кривая Серпинского, точнее – ее вариант, H-индекс – подходит для формирования расписания значительно лучше, чем построчный алгоритм. Однако, я не доказал, что вариант расписания с применением H-индекса является оптимальным. На самом деле, можно легко проследить, что при определенных объемах памяти, например, в упражнении по ручному распределению, можно добиться (немного) лучшего результата, чем при применении H-индекса. Рольф Нидермайер, Клаус Рейнхардт и Петер Сандерс, изобретатели H-индекса, убедительно доказали, что он является асимптотически оптимальным.
Означает ли это, что мы должны отказаться от всех обходов матриц, основанных на вложенных циклах – то есть, от построчного построения расписаний – и заменить их обходом на основании H-индекса? Вероятно, нет. Проделана огромная работа по оптимизации таких циклов в компиляторах, для тонкой настройки их механизмов кэширования. Показанный здесь эксперимент учитывает лишь два очень частных случая, а также основывается на таких допущениях о поведении кэша, которые не соблюдаются во многих системах.
Например, кэши процессоров обычно применяют иные стратегии замены. При заполнении до отказа процессор не затирает наименее используемые элементы, а действует сложнее. Однако, кривая Серпинского и H-индекс действительно пригодились во многих приложениях, связанных с интенсивными вычислениями (области применения – от обработки изображений до баз данных). Возможно, эти кривые будут полезны и вам.
Размеры данного поста не позволяют рассмотреть практическое применение этой кривой. Внимательные читатели могли заметить, что во всех примерах я использовал только такие количества станций, которые являются степенью двух. Это неслучайно: H-индекс хорошо подходит именно для работы с такими степенями. Правда, можно адаптировать индекс и для работы в более крупных масштабах, таким образом, что расписание, в основном, будет соответствовать H-индексу. Возможности практического применения и их эмпирическая оценка требуют дополнительных исследований.
Постскриптум
Поскольку недавно я выполнял проект на Elm, мне было очень интересно писать эту статью. Работа с таким новым языком по определению очень интересна: одной рукой вы творите все новые способы решения задач, а другой – снова и снова изобретаете велосипед. Начинаешь ценить то время, которое было затрачено на написание библиотек для других, более зрелых языков. Например, я потратил массу времени на разработку графиков, порой выдавая просто монструозный код.
Можете ознакомиться с кодом здесь, но учтите – врачи не рекомендуют!
Гидеон Смедлинг
Источник





Релоцировались? Теперь вы можете комментировать без верификации аккаунта.